Considering how many fools can calculate, it is surprising that it should be thought either a dffficult or a tedious task for any other fool to learn how to master the same tricks. Some calculus tricks are quite easy. Some are enormously difficult. The fools who write the textbooks of advanced mathematics --and they are mostly clever fools-- seldom take the trouble to show you how easy the easy calculations are. On the contrary, they seem to desire to impress you with their tremendous cleverness by going about it in the most difficult way.
Being myself a remarkably stupid fellow, I have had to unteach myself the difficulties, and now beg to present to my fellow fools the parts that are not hard. Master these thoroughly, and the rest will follow. WHAT ONE FOOL CAN DO, ANOTHER CAN.
Silvanus P. Thompson (Calculus Made Easy (London: Macmillan & Co., 1961)
Mathematics is not the only subject where people start with the more difficult concepts first and then work their way back to the simpler ones. People being introduced to the subject of cancer are first confronted with the complex concepts, and often never get near the simpler ones. The virus theory of cancer, or what cancers look like under the microscope, or how they spread, is extremely complicated. In contrast, an overview of the dynamics of growth can be fairly simple.
It is much simpler to think of things in a frozen static state than to think of them in motion. People (including a majority of cancer biologists) prefer to think of things in discrete stages because their minds can handle static concepts more easily. No one has any particular difficulty with the concept of an automobile moving at a rate of speed, or of someone running at 12 miles per hour; yet we prefer to freeze time by saying that "he ran the mile in five minutes." One of the aims of the study of biology is to discover what "reality" is and isn't --and one thing that it isn't is things standing still. Living things are always in some form of motion and it is preferable, if possible, to deal with them while they are in motion.
As with speed and distance, it is important to distinguish between growth per se and growth rate. When we talk about rate we consider the factor of time. To say that a lump under the skin has grown from the size of a marble to the size of an orange is to describe growth. To say that it has grown from the size of a marble to the size of an orange in one month is to describe the growth rate. It is often hard for people to understand that while the growth rate may remain constant, the actual amount of growth (in mass) may appear to explode. The growth rate of the tumor may be slow and fairly constant; yet, when it appears to go from the size of a marble to the size of an orange, or worse from the size of an orange to the size of a watermelon, people would ordinarily think that something has changed in the tumor; whereas in reality, the only thing that has happened is that the tumor has continued to grow at the same logarithmic (exponential) rate. In other words, one cell divided into two at a constant rate resulting in growth by doubling (see the next chapter).
The general principle of growth is the same for tumors as it is for populations of people, field mice, bacteria, or molecules. If you understand this general principle, you have the key to understanding what happens in cancer, population explosions, and some aspects of physical chemistry.
What is this principle around which cancer research and the study of growth can revolve? I'm almost ashamed to mention it, it's so simple and obvious. It is this:
THE RATE AT WHICH SOMETHING GROWS IS EQUAL TO THE RATE AT WHICH THINGS GO IN MINUS THE RATE AT WHICH THINGS COME OUT.
I have illustrated this by a little diagram (which I borrowed from the geneticist Curt Stern who used it to describe genetic equilibrium).
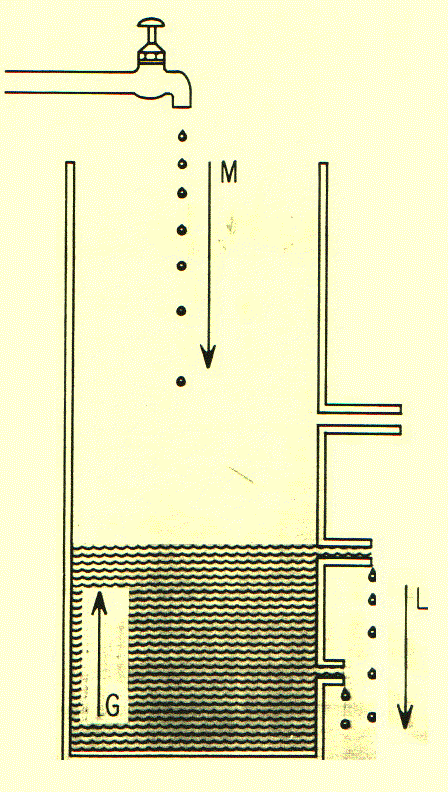
This diagram shows that if you pour water into a pail that has holes in it, the rate at which the pail fills up is equal to the rate at which water goes in minus the rate at which water goes out. It won't do to let it stay like that; it's too pedestrian to merely verbally explain the obvious --we have to put it into mathematical form. The form is
If you substitute human birth rate for M and human death rate for L, then G is the rate of population growth.
Observe that I am using the word growth to describe the end product. We all understand what growth means when we watch a child grow from 7 pounds to 150 pounds in a period of sixteen years. This "growth" that we observe is the result of cells being produced and cells being lost. When something "grows" or "shrinks," what we observe is the end product of an interaction between cells that are being produced and cells that are being lost.
It is important to remember that the growth rate has to be continuously greater than zero to have a cancer or a human population explosion. There are always short spurts of growth that either stop or regress later on. Our normal response to injury or infection involves temporary growth spurts. The total picture over a period of time is what is important, not momentary changes.
The principles of growth that cancers obey are no different from those for embryos, or cultures of bacteria, or populations of people or mice. These principles of growth are the same for both "normal" and "abnormal" growth. This is not surprising, since the border between normality and abnormality is an arbitrary line which divides the usual from the unusual or the desirable from the undesirable. The same kind of uncertainty that exists in separating the sane from the insane also exists in separating the normal tissues from the cancerous ones.
A many-celled organism always has things happening within it. Cells are always dividing, and cells are always being lost, usually at a phenomenal rate. Instead of a static state, we have what is called dynamic equilibrium. When you see that your left thumb has not gotten any bigger in the last several years, it does not mean that cells are not being reproduced, and discarded, but that the rate at which cells are being produced is the same as the rate at which cells are being lost. To prove this to your own satisfaction, just observe your fingernail. Unless you chop off the end of it, it grows. It is up to you to take care of the "LOSS" part of the equation with a pair of nail clippers. You can calculate how fast the cells in your nail bed are dividing by measuring nail growth and knowing the height of the cell (L=O; therefore, G=M). The skin of your thumb, on the other hand, pretty well takes care of itself by obligingly sluffing off into the environment. It's called dandruff if clumps of cells sluff off on the top of your head. The magnitude of this skin cell loss can be appreciated by people who have had a limb in a cast for a period of time. When the cast comes off, there are sheets of dead skin that have sluffed off and had no place to go. We could try to solve the dandruff problem in the manner of the Hiawatha parody, "With the skin he made him mittens and he put the fur side inside and he put the skin side outside." You can get away from this with dead skin, but with live skin the cells continue to divide, continue to sluff off, only they have no place to go and we have what is called a cyst, which continues to grow until it is either removed or breaks through to the outside and spills its contents. This cyst looks like a tumor from the outside, but differs from one because there is little or no real increase in the number of living cells. The thing that increases the size of the cyst is the accumulation of dead cells and debris on the inside. This can cause trouble by pressing on things; and a cyst of the brain can be very serious. Ordinarily, however, cysts are just a nuisance to everyone but the surgeon, who can make part of his living by removing them.
We generally distinguish cysts from true tumors even though they superficially look about the same from the outside. To be a true tumor, there has to be an increase in the number of live cells present that has to continue until there is a visible mass that hadn't ought to be there. For a tumor to be malignant, it has to continue to grow until it kills the person or the animal bearing it. Some physicians and scientists don't consider a tumor to be malignant if it just continues to grow, provided that it stays in the same place and the cells don't move into tissues and organs where they don't belong. It is easy to see that the tumor that stays in one place and can be removed from an individual (in much the same way that you can take a nut out of its shell) is not particularly dangerous, provided that it is removed. At the same time, any tumor that continues to grow can become a hazard by pressing on vital organs. A tumor that reaches a certain size and then stops growing, or grows at such a slow rate as to be barely perceptible and stays in one place, is clearly benign; and it may be irrelevant whether it is removed or not.
Certain types of cells, such as the white blood cells, whose normal behavior requires them to circulate in the body, automatically become killers if the total number of cells continues to increase. It is not necessary that they change their behavior and invade organs where they're not supposed to be, because they are supposed to be everywhere. When these cells continue to circulate in the blood stream, a condition is produced which is called "Leukemia" (white blood). This will be discussed later.
A tumor that continues to grow and does not invade surroundlng tissue or metastasize can be just as deadly as one that does, if it is located in a vital area. Before the advent of chest surgery, any progressively growing tumor of the lung was fatal because it could not be removed, and would eventually crowd out the lung to the point where the individual bearing it could no longer breathe. The same thing is true of some tumors of the brain, in which the tumor cannot be reached without killing the individual bearing it. On the other hand, a tumor with the ability to spread is harmless if it can be removed before that spreading has actually occurred. This is very often the case with small tumors of the skin. As the words are used today, calling a tumor malignant or benign tells the individual bearing it very little about his future. The terms "curable" and "incurable," and the probabilities of a tumor being one or the other, are far more relevant if you happen to be in the business of predicting the future, or if you happen to be the patient.
This way of looking at cancer as a continuing dynamic process instead of a static state is very useful when you try to understand what cancer is. In the chapters to come, I will point out how this concept of "cancer as a dynamic process" is related to predicting the future of cancer research with regard to the probability of finding a "cure."
This ability of cells to reproduce and to die is the very basis of life. Without cells being born there would, of course, be no life. Without cells continually dying there would be no room on our planet for new life. This potential to reproduce also keeps our skin and intestine intact by allowing the repair of injuries. Imagine what would happen if every cut or scrape or infection that we received in a lifetime didn't heal. These miracles, which we take for granted, are of the same fabric that cancers are made of.
Ecologists speak of the balance between an animal species and its food supply. This ecological balance within the body is necessary for the well-being of an individual. If not enough cells are reproduced, then we are unable to repair an injury; and if too many cells are reproduced, we have a tumor. It is important to remember again, that not enough cells dying accomplishes the same end as having too many cells being born --again the concept of balance.
While the principle of growth is a very simple one, its actual application can be extremely difficult. There are many factors which determine how rapidly or how frequently cells divide, with the result that this process rarely remains constant. The same is true of cell loss, which is influenced by a large number of factors --not the least of which is the surgeon's knife. Sometimes, trying to apply this principle in an experiment can be like trying to thread a needle while riding a bucking horse.