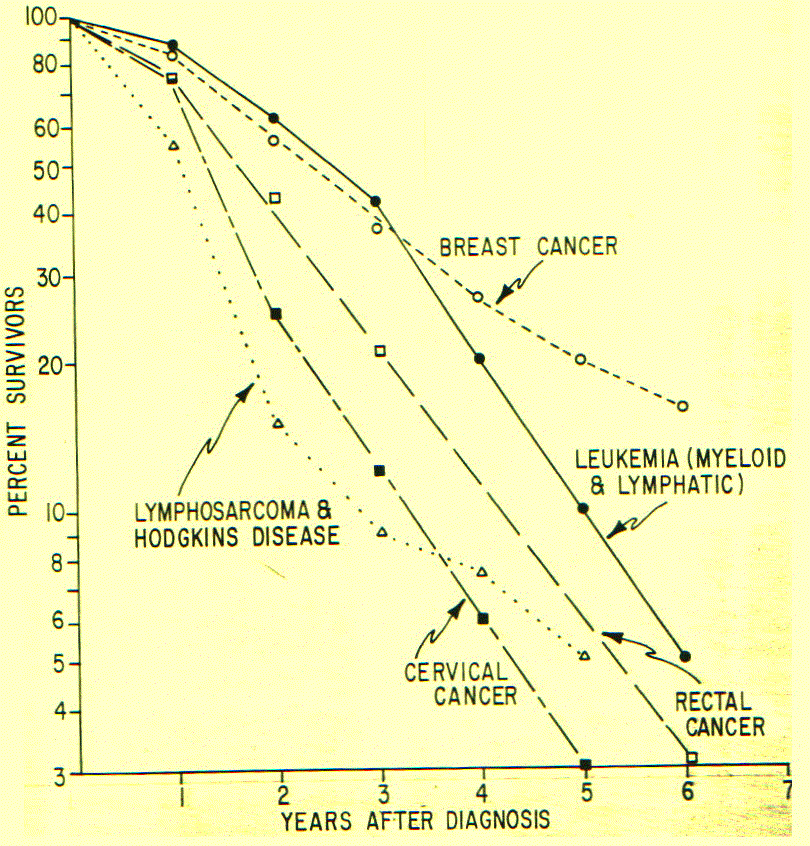
To give you some idea of what can be expected in untreated cancer, Figure 6 shows the survival curves for a number of common types of untreated cancer.
Removlng parts of people is
The surgeon's wondrous knack.
But once the part has been took out,
It's hard to put it back.
A fairly good principle in the treatment of tumors is the surgeon's law of "When in doubt, cut it out." Many people prefer to stew and fret about little lumps before finally making the decision to see a doctor. The rationale for this seems to be that "I am afraid that it is cancer and, if it is, I don't want to know about it." The delay simply prolongs the mental agony and endangers the person's life. If the operation is not dangerous, it never hurts to remove a tumor. If it is removed, you will be relieved of future worry should it turn out, as it usually does, to be of the benign variety. Should it he malignant, then the chances of a cure are much better if it is removed early. I am talking now about small growths on the skin or under the skin that can easily be removed with a local anesthetic. When it comes to tumors that require major surgery, that's another story. The danger of the operation has to be equated against the possibility of doing some good by it. This is a very difficult decision to make. The better the judgment and skill of the surgeon, and the judgment of the pathologist, the better the chances for the patient. Unfortunately, there is no foolproof way of determing either. (See chapter on How to Pick a Doctor.)
What is the relationship of the size of a tumor to its curability and to its tendency to metastasize? It is surprising, in view of the importance of this question, that so little fundamental research has actually been done in this area. It makes sense to remove a tumor while it is still small because (1) the surgery is much simpler, and (2) even if the tumor has a tendency to metastasize, the probability of catching the tumor before it has actually done so is greater.
There is some fairly good empiric evidence that the smaller the tumor is when it is removed, the better are the chances of survival for the patient. Survival in breast cancer treated with radical mastectomy is related to the size of the tumor when it was removed. If the tumor is less than 2 cm. (3/4 of an inch) in diameter, then the five-year survival is about 76%; if it is 2 to 5 cm. (3/4 to 2 inches) in diameter, the five-year survival is 55%; and if the tumor is 5 to10 cm. (2 to 4 inches) in diameter, then the five-year survival is about 25%
If most people knew what an amazingly large percentage of cancers are completely curable by surgery (the cure rates in some forms of cancer are over 90 percent), there would be no hesitation about going to a doctor and having the operation done as soon as possible.
I would like to make it clear that I am not advocating the removal of moles, birthmarks, and other common skin lesions. We all have some of these and, if we had them all removed, not only would we be covered from head to toe with band-aids, but every surgeon and physician in the country would be kept busy removing moles. What I am referring to are the moles, or whatever you call them, that have been doing nothing for a long time which start to grow; or moles that are in areas where they are continually subject to irritation. What I should say is, If it's starting to grow, or if it is bothering you, cut it out. There is little point to "prophylactic surgery" per se. We know that we could prevent all breast cancer by removing the breasts of all women at puberty, but I don't think that anyone would advocate this as a routine procedure.
The major problem in evaluating the effect of treatment on cancer is the fact that the course of the disease is so damnably unpredictable. One woman with completely untreated breast cancer may succumb six months after diagnosis, while another may live beyond five years. In untreated breast cancer, 85% of the women diagnosed as having it will live for a year; 50% will live for two and a half years, and 20% will live past five years (the usual criterion for the cure of the disease). Every surgeon who has treated breast cancer knows that some of his cases succumb very quickly after surgery, while some survive for relatively long periods of time. He has no idea whether extended survival is because of his treatment, or in spite of it. The tragedy is that information on the effectiveness of surgical treatment is not that difficult to obtain. All that is necssary is that some funds be made available to the right people to do, in surgery, what is presently being done in the evaluations of the chemical treatments for cancer.
To give you some idea of what can be expected in untreated cancer, Figure 6 shows the survival curves for a number of common types of untreated cancer.

Figure 6
Survival of people with untreated cancer. (Data adapted from M.B.Shimkin, "Natural History of Neoplastic Disease," The Physiopathology of Cancer 2nd ed., edited by F. Homburger, pp.855-871 (N.Y., Harper and Rowe, 1959)
This method of graphing survivors is very useful, because the slope of the line at any particular point is the death rate. The reason that we use the logarithm of the percent survival is to correct for the fact that we have a continually decreasing population. For example, if we started out with 100 people, at the end of a particular interval we would have 90, then 70, and so on. In order to have the slope of the curve equal the mortality rate, we use a logarithmic scale to correct for this decrease. The use of logarithms is not simply a gimmick, but is a valid method of correcting for the fact that the population at risk is continually decreasing.
We can view the curve as we do a sleigh riding hill, with the steepness of the slope being proportional to the speed of the sled, or the risk of dying. Take breast cancer, for example: you will find that you sort of have to push your sled a bit to get started over the first year (there is not too much risk of dying In that period of time), and then it starts going down pretty fast, with the risk of dying increasing at a fairly rapid rate. By the time five years have arrived, approximately 80% of the untreated cases will have succumbed. The slope does not change too much, even at the five-year point.
If, however, you compare this curve with cases of breast cancer treated by surgery (Figure 7), you find that the slope is much more gradual, with about 60% of the people surviving for five years instead of the 20% in the untreated group. When the slope got to be about the same as the general death rate of people in the same age group that did not have breast cancer, then a person is "home free." In other words, if a woman has breast cancer and is treated, and she makes it past six or seven years, she is pretty well out of the woods. In fact, if she makes it to five years, and the doctors can detect no sign of metastasis she is also pretty well out of the woods.
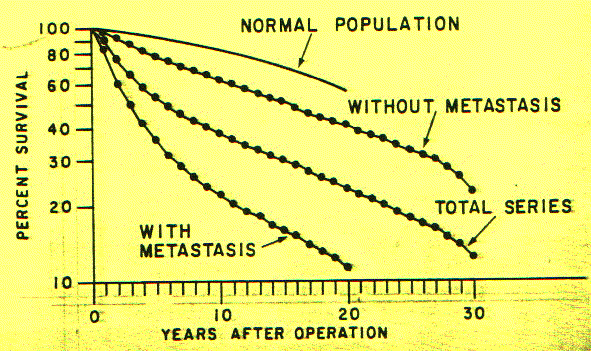 Figure 7
Figure 7
The survival of patients with treated breast cancer, compared with the survival of the normal population in the same age group. (From J. Berkson et al., "Mortality and Survival in Surgically Treated Cancer of the Breast: A Statistical Summary of Some Experience of the Mayo Clinic." Proceedings of the Staff Meetings of the Mayo Clinic
32 [1957]: 647:670.
So, if we wanted to find out whether a certain treatment for cancer was effective or not, all that would be necessary would be to first draw a curve of treated cases and compare it with the curve for the untreated ones; and, second, once we have a treatment that appears to work, then we can compare the curves for individuals treated in this way with the curves for individuals treated by any new treatment. It is important to make sure that the composition of people in the groups being compared is truly comparable. To do this, the ages of the patients, the method of selection, the histologic tumor type, the stage of the development of the disease, all have to be comparable in the groups being compared. It looks complicated, but it is nowhere near as difficult and as complicated as it sounds. If an experimental treatment is used, and it is compared with a standard curve (usually the best available current treatment) and it is found that the curves overlap, it means that the addition to the treatment is ineffective. If the curve of the treated sample falls below the curve for the others, then the treatment is worse; and if the curve is above the standard curve then the treatment is better. The more times the experiment is repeated with the same results, the more believable the results become. The medical literature is full of reports where a physician tries a treatment on five or ten cases and reports superb results, which could not subsequently be obtained by others. It is sad, but true, that while the physician is the man best equipped to treat people with cancer, he is generally poorly equipped to evaluate the results of his treatment. In fact, because of built-in bias (he wants the treatment to succeed) he should leave the evaluation to unbiased statisticians. This is being done in some of the better cancer research institutes; but with their limited number of cases it will take them a lot longer to get the information needed than would a cooperative program involving many large hospitals.
I would like to anticipate my own conclusions, and point out that a cure is not just around the corner and we had better start perfecting the tools at hand so that, even if we can't save too many more lives, we can at least reduce some human suffering caused by ineffective treatments.